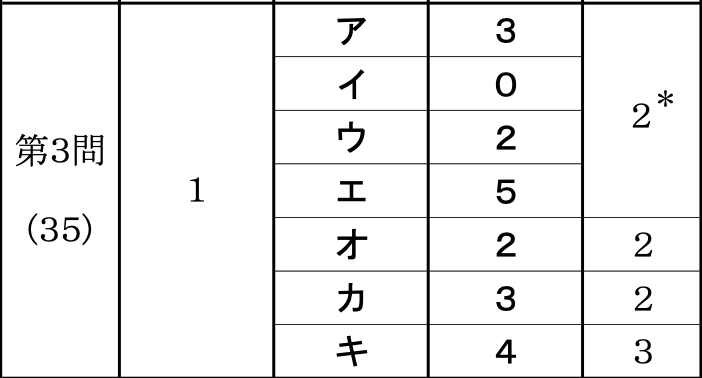
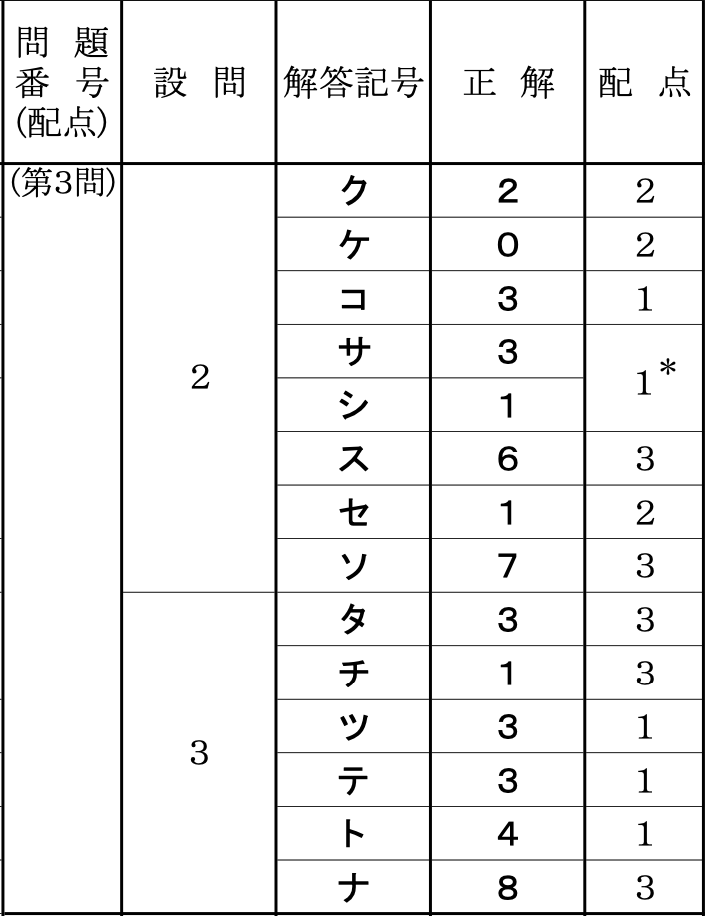
問題
正解
解説
図1ゲーム画面で実際にどのように動くかイメージしながら解けばそんなに難しくない問題でした。
問1
アイウエ
「各ロープを5mずつ降りるという動かし方を考えた」とあります。
よって、
1本目 55m → 50m
2本目 50m → 45m
3本目 45m → 40m
4本目 40m → 35m
5本目 35m → 30m
6本目 30m → 25m
7本目 25m → 20m
8本目 20m → 15m
9本目 15m → 10m
10本目 10m → 5m
11本目 5m → 0m
と降りてくことになるので、6本目は30mから25mまで降ります。
キ
tokutenが加算されるのは、現在の高さから5m下がるまでに、リボンがある場合です。
そのため、条件は takasa – 5 <= Ribon[i] <= takasa を満たす場合ということになります。
図2のプログラムをPythonで書いてみました。表1リボンの高さが、配列Ribonに対応しているのですが、配列番号が1から始まるのでそこだけ注意が必要ですね。普段DNCLでは配列番号0から始まることが多いのですが、今回は1からになっています。表記を合わせるために、配列番号0の場所には0を入れています。また、tokuten += 1といった書き方もできますが、DNCLに合わせた書き方をしています。
Ribon = [0,55,53,31,37,37,22,13,19,25,16,0] # 今回はスタートが1なので、配列番号0には0を入れています。
tokuten = 0
takasa = 55
for i in range(1, 12):
if Ribon[i] >= takasa - 5 and Ribon[i] <= takasa:
tokuten = tokuten + 1
takasa = takasa - 5
print('得点は', tokuten, '点')【実行結果】
得点は 4 点
問2
クケコサシス
【新しい動かし方】というものが登場しました。毎回5m下がる降り方ではなく、各ロープでリボンに触れるまで降りて、リボンに触れたら次のロープに移るそうです。
Ribon[i]がtakasa以下の場合に、takasaをRibon[i]にすればよいです。
図3のプログラムをPythonで書いてみました。
Ribon = [0,55,53,31,37,37,22,13,19,25,16,0]
tokuten = 0
takasa = 55
for i in range(1, 12):
if Ribon[i] <= takasa:
tokuten = tokuten + 1
takasa = Ribon[i]
# print('i', i, 'tokuten', tokuten, 'takasa', takasa)
print('得点は', tokuten, '点')【実行結果】
得点は 6 点
表2を出力する場合はコメントアウトを外してください。
【実行結果】
i 1 tokuten 1 takasa 55
i 2 tokuten 2 takasa 53
i 3 tokuten 3 takasa 31
i 4 tokuten 3 takasa 31
i 5 tokuten 3 takasa 31
i 6 tokuten 4 takasa 22
i 7 tokuten 5 takasa 13
i 8 tokuten 5 takasa 13
i 9 tokuten 5 takasa 13
i 10 tokuten 5 takasa 13
i 11 tokuten 6 takasa 0
セソ
降りすぎると損をする場合があるということで、限度を決めることにしたそうです。
今回は 定数GENDOが登場し、限度は20mとなっています。
その場合、Ribon[i]がtakasa以下であり、かつ、takasa – Ribon[i]がGENDO未満のときにtokutenが加算されるように条件文を書きます。また、最後のロープではかならず0mまで降りるようにするので、i = 11の際には強制的に高さを0（Ribon[11]）にしてあげる必要があります。
Pythonプログラムは以下です。
Ribon = [0,55,53,31,37,37,22,13,19,25,16,0]
GENDO = 20
tokuten = 0
takasa = 55
for i in range(1, 12):
if ( Ribon[i] <= takasa and takasa - Ribon[i] < GENDO ) or i == 11:
tokuten = tokuten + 1
takasa = Ribon[i]
print('得点は', tokuten, '点')【実行結果】
得点は 7 点
問3
タ
i本目のロープに触れた際の最高得点をKokomade[i]とするそうです。
Kokomade[i]の求め方は、iより小さいすべてのt（Kokomade[t]）のうち、一番値が大きいものに+1するというようになっています。
そのため、Ribon[t]がRibon[i]以上の高さにあるすべてのtのうち、Kokomade[t]の値が最も大きいものを使います。
Pythonプログラムは以下のようになります。
Ribon = [0,55,53,31,37,37,22,13,19,25,16,0]
Kokomade = [0] * 12 # 配列Kokomadeを宣言しておく。ロープ番号に合わせるために、配列番号0は使わないので0~11で宣言
Kokomade[1] = 1
for i in range(2, 12):
saikou = 0
for t in range(1, i):
if Ribon[t] >= Ribon[i] and saikou < Kokomade[t]:
saikou = Kokomade[t]
Kokomade[i] = saikou + 1
# print(Kokomade[i], end=',')
print('獲得可能な最高得点は', Kokomade[11], '点')【実行結果】
獲得可能な最高得点は 8 点
表3を埋める場合は、コメントアウトを外してください。
【実行結果】
2,3,3,4,5,6,6,5,7,8,
生成日時: 未生成
生成日時: 未生成
高校生向け解説：情報科試験問題
この問題は、情報科の中でもプログラミング的思考を問う問題です。具体的な内容は、ゲームのルールを理解し、そのルールに基づいて最適な戦略を立案することです。問題文は一見複雑に見えますが、一つずつ丁寧に読み進めていけば理解できます。
問題1この問題は、ループ処理と条件分岐を理解しているかを問うています。
背景知識 ループ処理: 同じ処理を繰り返すプログラムの構造。 条件分岐: 条件によって処理を分岐させるプログラムの構造。 解答の導き方1. 問題文の理解: Aさんがロープを引っ張ってゴールを目指すゲームのルールを理解する。 2. 変数の定義: ループの番号（`tokuen`）、ロープの長さ（`takasa`）、ロープを引いた回数（`ka`）などの変数を定義する。 3. ループ処理: ループの番号が1から11まで繰り返される処理を記述する。 4. 条件分岐: ロープを引いた回数によって、ロープの長さが変化する処理を記述する。 5. 最終的な処理: ループが終了した後の処理を記述する。
解答例``` tokuen = 0 takasa = 55
for i in range(1, 12): if i <= 11: ka = tokuen + 1 takasa = takasa - 5 print(f"ループ{i}回目: ロープの長さ={takasa}m") else: print("ゴール!") ```
関連する情報科の概念 アルゴリズム: 問題を解決するための手順 フローチャート: アルゴリズムを図式化した表現方法 変数: 値を格納するための箱 問題2この問題は、データの処理と条件分岐を理解しているかを問うています。
背景知識 データの処理: データを加工したり、分析したりすること。 条件分岐: 条件によって処理を分岐させるプログラムの構造。 解答の導き方1. 問題文の理解: Aさんが新しい引っ張り方のルールを理解する。 2. 変数の定義: ループの番号（`tokuen`）、ロープの長さ（`takasa`）、引っ張った回数（`ka`）、ゲームの終了条件（`GENDO`）などの変数を定義する。 3. ループ処理: ループの番号が1から11まで繰り返される処理を記述する。 4. 条件分岐: 引っ張った回数によって、ロープの長さが変化する処理を記述する。 5. ゲーム終了条件: `GENDO`の値が満たされたらゲーム終了とする処理を記述する。
解答例``` tokuen = 0 takasa = 55 GENDO = 20
for i in range(1, 12): if i <= 11: ka = tokuen + 1 takasa = takasa - 5 if takasa < GENDO: print(f"ループ{i}回目: ロープの長さ={takasa}m, ゲーム終了!") break else: print(f"ループ{i}回目: ロープの長さ={takasa}m") else: print("ゴール!") ```
関連する情報科の概念 データ型: データの種類（数値、文字列など） 演算子: データを操作するための記号 比較演算子: データを比較するための記号 問題3この問題は、アルゴリズムの設計と最適化を理解しているかを問うています。
背景知識 アルゴリズム: 問題を解決するための手順 最適化: アルゴリズムをより効率的に改善すること 解答の導き方1. 問題文の理解: Aさんが、より効率的にゲームを進めるための新しい戦略を考案する。 2. 変数の定義: ループの番号（`Kokomode`）、ロープを引いた回数（`saikou`）、ロープの長さ（`Ribbon`）、ゲームの終了条件（`GENDO`）などの変数を定義する。 3. アルゴリズム: 新しい戦略に基づいて、ロープを引く手順を記述する。
生成日時: 2024-08-27 11:29:49
